摘要

在地球和空间科学探测领域，应用广泛的磁强计无一例外地采用亥姆霍兹线圈产生反馈弱磁场。但磁强计测量精度的进一步提高，受限于该反馈磁场的均匀度。

本项目提出了一种产生高均匀区磁场的方法，在数学建模中创新性地采用轴向、径向两个变量参与计算，构建了更为全面的磁场模型，利用改进的PSO 智能优化算法将遍历法与泰勒展开法相结合，在保证精度的前提下极大地提升了效率，并在ComsolMultiphysics 中建立模型，获得了磁场 均匀区的径向占比达到 的高阶线圈阵列，与亥姆霍兹线圈相比均匀区增大1 倍。同时该方法也适用于二维、三维均匀磁场的产生，具有高均匀性与三维化的特点。

本研究在沿用前人研究思路的同时，在每个步骤均加入了新的思考，最终完成了对性能的提升，并主要围绕磁强计作为应用场景进行设计，将其高均匀区和小型化等要求作为主要问题进行研究突破。优化后的线圈具备着高均匀度、微型化、可三维化等优点，若应用于磁标定、磁测量领域，将会对精度有着较大提升，并且集百家之长的设计令其有更加广泛的应用空间。综合而言，本项目在满足了最初设计理念的同时，还可以助力磁场科学的进步，为更多的科学研究赋能。

关键词：高均匀磁场，智能优化算法，线圈阵列，磁通门磁强计

Abstract

In the field of Earth and space science exploration, widely used magnetometers invariably use Helmholtz coils to generate a feedback weak magnetic field. However, further improvement of the measurement accuracy of magnetometers is limited by the uniformity of this feedback magnetic field.

This project proposes a method to generate a magnetic field with high uniformity region, innovatively adopting two variables of axial and radial direction in mathematical modelling to participate in the calculation, constructing a more comprehensive model of the magnetic field, combining the traversing method with the Taylor expansion method by using the improved PSO intelligent optimisation algorithm, which greatly enhances the efficiency under the premise of guaranteeing the accuracy, and building the model in Comsol Multiphysics, a higher-order coil array with a radial share of in the uniform region of the magnetic field is obtained, and the uniform region is increased by a factor of 1 compared with the Helmholtz coil. The method is also applicable to the generation of two- and three-dimensional uniform magnetic fields with high uniformity and three-dimensionality.

In this study, while following the ideas of the previous research, new thinking is added in each step to finally complete the improvement of the performance, and the design is mainly focused on the magnetometer as an application scenario, and its requirements such as high uniformity zone and miniaturisation are taken as the main problems for the research breakthrough. The optimised coil has the advantages of high uniformity, miniaturisation and three-dimensionalisation, which will improve the accuracy if it is applied in the field of magnetic calibration and magnetic measurement, and the design that combines all the strengths of the magnetometers will make them have a wider application space. All in all, this project can help the progress of magnetic field science while fulfilling the original design concept, and empower more scientific research.

Keywords: Highly uniform magnetic field, Intelligent optimisation algorithm, Coil array, Magnetom

绪论

在地球和空间科学探测领域，广泛应用的磁通门磁强计无一例外地采用亥姆霍兹线圈产生反馈弱磁场，但磁强计测量精度的进一步提高受限于反馈磁场的均匀度。而线圈的参数决定了产生磁场的特性，所以需要对磁场线圈的参数进行多目标优化，使其产生的磁场满足高均匀区等特点。

学者们对线圈展开了大量的研究。王倩等在传统亥姆霍兹线圈的基础上提出了双锥式均匀磁场发生器，该双锥式均匀磁场发生器由多对半径不同的共轴亥姆霍兹线圈构成，其产生的磁场范围和精度都优于亥姆霍兹线圈[1]。Wang 等提出半径相同的3 圆形线圈组的等径方式，张引科等提出3 圆形线圈组的等流方式，这2 种方法对改善亥姆霍兹线圈磁感应强度的均匀性都有较为显著的效果，其中等流方式产生的磁场均匀性要比等径方式略好[2-4]。胡朝晖等提出了由半径相同的圆形线圈组成的圆柱形线圈组在任意线圈数下各参数的计算方法，并给出随着线圈组数从2 增加到9，磁场均匀度不断增加，均匀度小于等于 和 的区域面积都基本呈线性增大[5]。

上述设计得到的磁场均匀度和均匀区范围均优于亥姆霍兹线圈，但也有其局限性：更多对线圈会占据更大的体积，用公式计算磁场强度的计算量也在增加，方程求解更加困难。随着计算能力提高，学者们将非线性方程求解线圈参数转变为非线性优化问题。目前，常用的智能优化算法有遗传算法、粒子群算法、模拟退火算法等。LYU 等提出一种基于智能优化算法的多线圈优化设计方法，其结果要优于传统求导寻优[6]。Everett 等提出了密绕球形线圈，其均匀性优于亥姆霍兹线圈，并且所占体积更小，节省了更大的空间，但要求尽可能无限多的匝数[7]。Pang 等利用智能优化算法得到了三维球形磁场线圈，它由三个相互垂直的球形线圈组成，其均匀度和均匀区范围都有所提高，并且可以在三个坐标轴方向上提供高度均匀且磁场性能一致的三维磁场，也满足小体积的需求[8]。

本项目提出了一种产生高均匀区磁场的方法——同轴高阶线圈阵列。通过数学建模与粒子群智能优化算法设计的高阶线圈阵列获得了横向达到0.63、纵向达到0.17 的 均匀区归一化半径，与亥姆霍兹线圈相比横向均匀区、纵向均匀区均有所扩大。同时该方法也适用于二维、三维高均匀磁场的产生，具有高均匀区与三维化的特点。

本文的创新点主要有以下几项：

●数学建模中创新性地采用轴向、径向两个变量参与计算，构建了更为全面的磁场模型，对目标函数有更精确的推导。

●由于径向变量r 的加入使得计算难度提升，本项目利用改进的PSO 优化算法，对使用遍历法与泰勒展开法相结合得到的目标函数进行优化，直接对不同点磁场强度进行比较，在保证精度的前提下极大地提升了效率。

●亥姆霍兹线圈 均匀区的归一化半径为0.31，优化后的线圈则为0.63。从结果上而言， 均匀区占比提升一倍。

本项目在沿用前人研究思路的同时，在每个步骤均加入了新的思考，最终完成了对性能的提升，并主要围绕磁强计作为应用场景进行设计，将其高均匀区和小型化等要求作为主要问题进行研究突破。优化后的线圈具备着高均匀度，微型化，可三维化等优点，若应用于磁标定、磁测量领域，将会对精度有着较大提升，并且集百家之长的设计令其有更加广泛的应用空间，综合而言，本项目在满足了最初设计理念的同时，还可以助力磁场科学的进步，为更多的科学研究赋能。

一、线圈磁场的数学模型

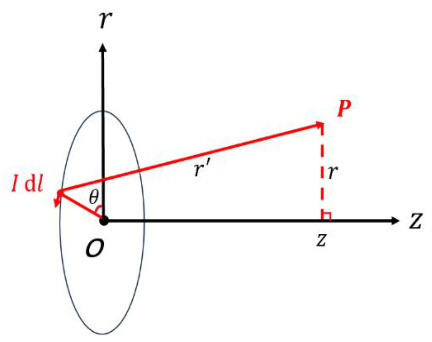
先考虑单个线圈在空间中产生的磁场，如图1 所示。


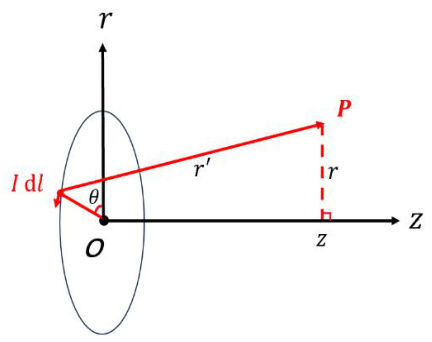
图1 空间中的单个线圈

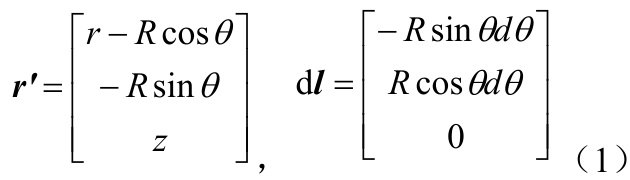
设线圈半径为R，圆心位于O 点，是线圈上的任意一段电流元. P 是空间中的任意一点,P 与 轴的距离为r，与线圈所在平面的距离为 。在空间直角坐标系中，由几何关系易得：

由毕奥-萨伐尔定律，电流元 在点P 处产生的磁场， 对θ积分可得：

其中 。

通过奇偶性分析得到 ，故磁场只有、 分量，在柱坐标系中可视为 、$ 分量。对 和 进行泰勒展开，得到：

此即为单个线圈在空间中任意一点 处所产生的磁场表达式。对于相距为d 的两个共轴线圈（即一组亥姆霍兹线圈），其磁场可以视作位于 处的两个单线圈磁场的叠加。相似地，对于 组相距为 ）的共轴线圈，其磁场可表示为：

其中

我们取 ， 、、，即考虑由8 对线圈所产生的轴向磁场的二阶近似：

对其在原点附近进行以 为变量的二阶泰勒展开，所得磁场表达式可简写为：

其中的系数 为：

对于如图2 所示的共轴球形线圈，设球壳的半径为定值R（在下文中，R 取为 ），则第i 组线圈的半径 与球壳半径R、线圈间距 满足勾股定理：

将其代入式（7），就得到了共轴球形线圈最终的磁场表达式。

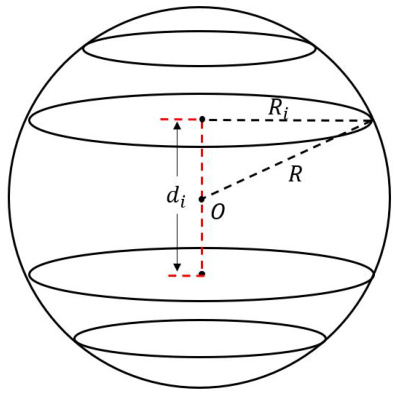图2 共轴球形线圈示意图

二、优化线圈参数

由式（8）可知，球形线圈磁场的数学模型共含有8 个未知参数（i=1,2,...,8），即目前8 组线圈在球壳中的分布位置是不确定的。我们的优化目标就是找到一组确定的线圈位置参数，使得球壳内的磁场分布最为均匀。根据以上模型，我们选择了粒子群优化算法来进行优化。

2.1 算法原理与流程

粒子群优化算法（Partical Swarm Optimization, 下称PSO 算法）初始生成一群随机粒子，代表一组随机解，然后通过不断迭代找到最优解。在每一次迭代中，粒子通过跟踪两个极值来更新自己：第一个是粒子本身所找到的最优解，这个极值称为个体极值；第二个是整个种群目前找到的最优解，这个极值是全局极值。

以我们的球形线圈模型为例，对于 ，总共需要优化8 个参数。假设在一个8 维的目标搜索空间中，有N 个粒子组成一个群落，其中第 个粒子的位置表示为一个8 维的向量：

这个位置向量就代表了一种可能的线圈分布方式。

第i 个粒子的速度也表示为一个8 维向量：

在迭代过程中，PSO 算法会使用下式更新 个粒子的位置向量和速度向量：

其中 分别是个体学习参数和社会学习参数， 是范围从0 到1 的两个随机数， 分别是个体极值和全局极值。

PSO 算法会比较每一代各个粒子所在的位置，并基于其中最理想的位置，对所有粒子进行迭代更新，而更新的方式就是用粒子原来的位置加上粒子走过的步长。通过这样的迭代，可以不断地发现更好的点，逐渐靠近使得磁场更均匀的一组线圈位置参数。

对应的PSO 算法步骤如图3 所示：


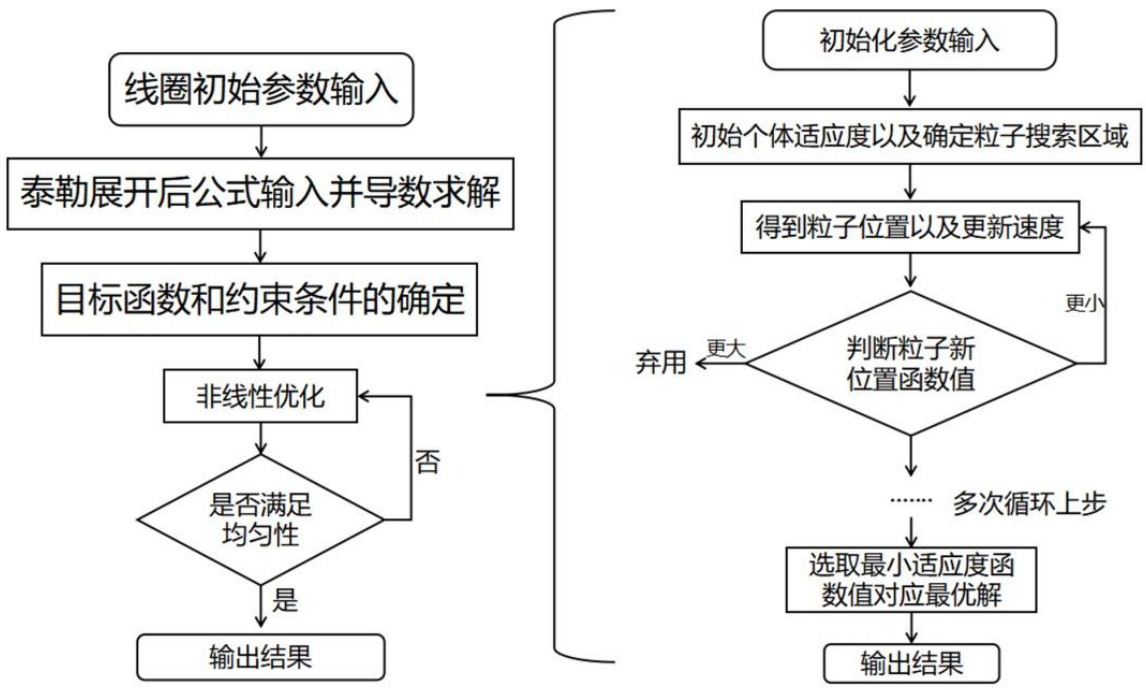
图3 优化设计流程图

1.初始化种群X，在8 维空间中随机位置生成N 个粒子，即 矩阵。

2.初始个体适应度。将每个粒子初始位置坐标代入适应度函数，得到初始个体极值和全局极值。

3.根据两个极值更新粒子速度和粒子的位置。在更新速度之前要进行速度边界检测，一般是当 时 。这么做的目的是防止速度太大，错过最理想的点。

4.计算各粒子新位置的适应度函数值，如果新位置适应度函数值更小，则更新个体极值。然后更新全局极值。

5.循环3、4 步。

6.达到迭代次数，终止迭代。

2.2 惯性权重的优化

我们采用了自适应惯性权重作为PSO 算法中的惯性权重：

惯性权重体现的是粒子继承先前的速度的能力：一个较大的惯性权值有利于全局搜索，而一个较小的惯性权值则更利于局部搜索。当各粒子的目标值趋于局部最优时，ω将增加；而各粒子的目标值比较分散时，ω将减小。

同时，对于目标函数值优于平均目标值的微粒，其对应的 较小，从而保护了该微

粒；反之对于目标函数值差于平均目标值的微粒，其对应的ω较大，使得该微粒向较好的搜索区域靠拢。

2.3 目标函数的选择

PSO 算法会通过目标函数的值来确定哪个粒子的位置最为理想。我们的优化目标是使磁场更加均匀，故所选取的目标函数应体现磁场的均匀度。由式（6），在以 坐标为变量、固定 坐标的情况下，总轴向磁场的表达式可简写为各线圈磁场的常数项与二次方项之和：

要使磁场的均匀度提高， 随 坐标的变化应尽可能小，即 项的系数之和应尽可能小。故取目标函数为：

其中目标函数f 包含了对 坐标的遍历， 取0 至 ，步长为 . r是归一化的权重系数，我们希望越靠近线圈中心的磁场越均匀，故 越小的位置权重系数越高。

通过上式，优化目标就转化为了让目标函数值通过不断迭代取到最小。

2.4 计算结果

经过多次运行程序，最终选取最小目标函数值所对应的最优解，也就是最优的线圈参数如下表所示：

表1 线圈位置参数最优解（单位：）

三、仿真模拟

在完成上述数学建模与算法优化后，我们进行了线圈建模与磁场仿真。本项目使用的建模软件为Comsol Multiphysics，所选用的研究类别为三维磁场稳态研究。在此基础上，我们完成了对于1）亥姆霍兹线圈、2）普通的等距球形线圈以及3）优化后的球形线圈这三者的建模，并进行了三者均匀区间的对比。

3.1 线圈建模

图4 的a、b、c 依次为亥姆霍兹线圈、等距球形线圈以及优化后的球形线圈的建模示意图。其中（a）亥姆霍兹线圈采用了令线圈间距d 等于线圈半径R 的构造方式，在此条件下，亥姆霍兹线圈磁场的均匀度被理论证明为最大[1]。（b）等距球形线圈是由在球壳上均匀分布的一组线圈构成的。（c）优化球形线圈是依据最优解所提供的线圈位置参数而构造的，每对线圈之间的间距为 。


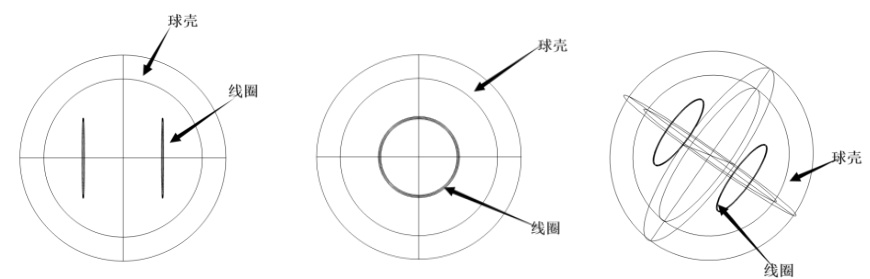
图4(a) 亥姆霍兹线圈结构示意图


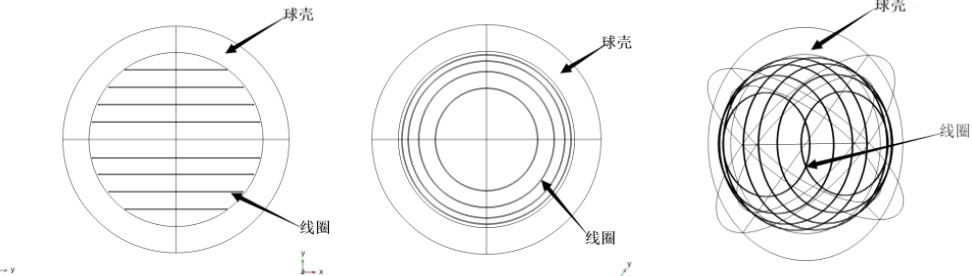
图4(b) 等距球形线圈结构示意图


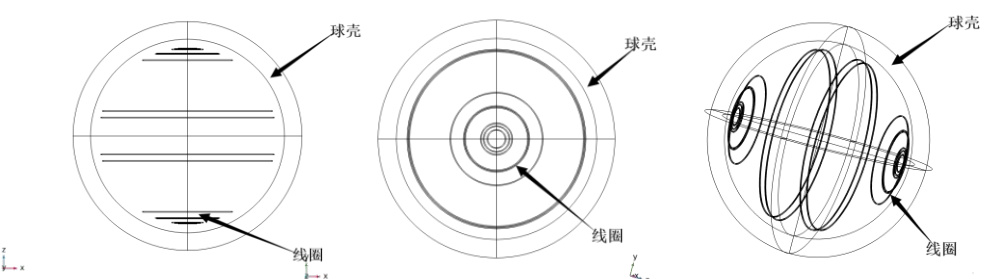
图4(c) 优化球形线圈结构示意图

通入电流后，三者的仿真磁场空间分布如图5 所示，磁场强度函数分布如图6 所示。


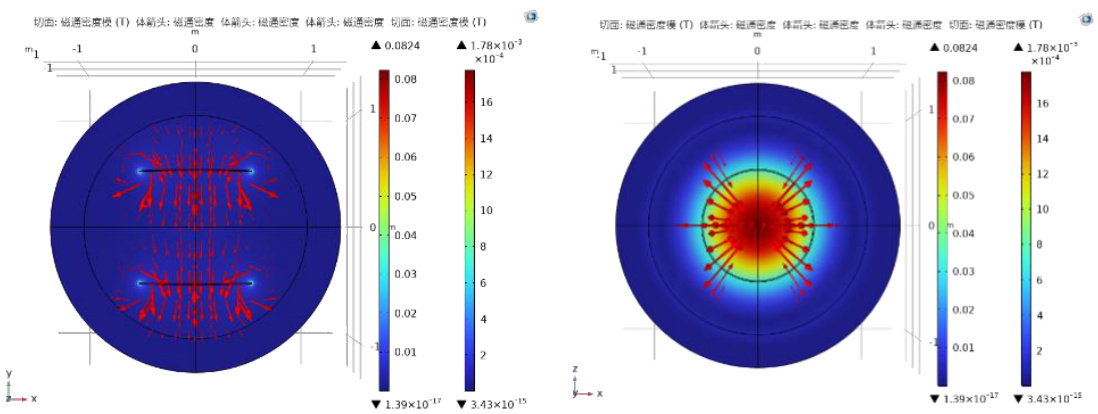
图5(a) 亥姆霍兹线圈磁场示意图


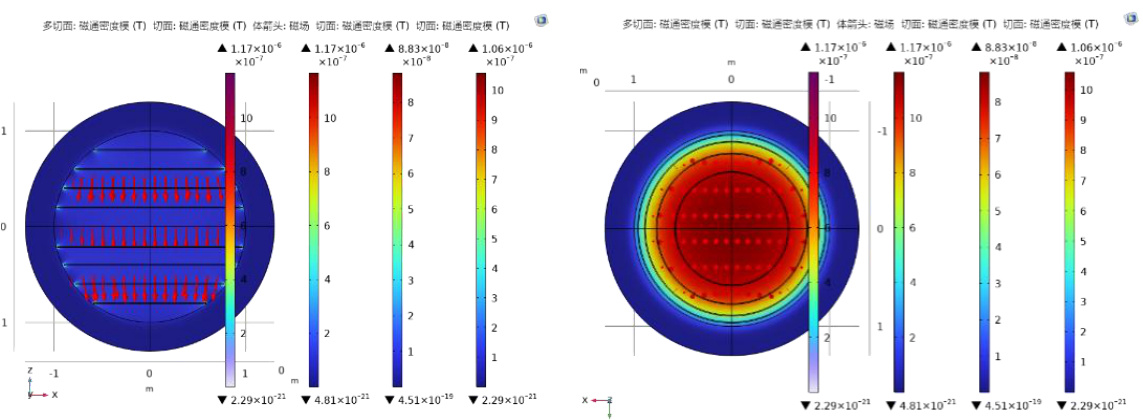
图5(b) 等距球形线圈磁场示意图


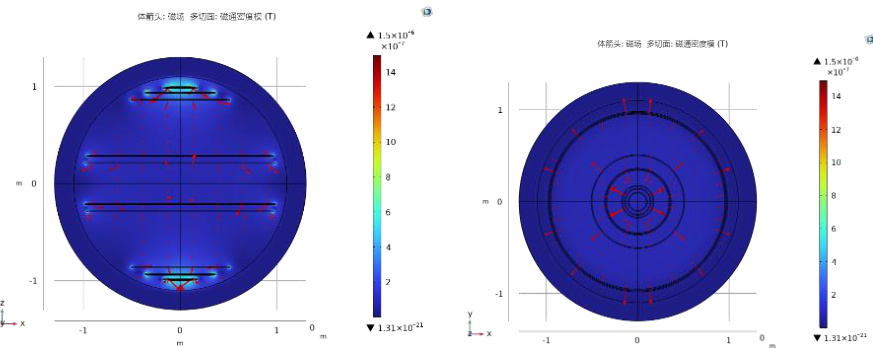
图5(c) 优化球形线圈磁场示意图


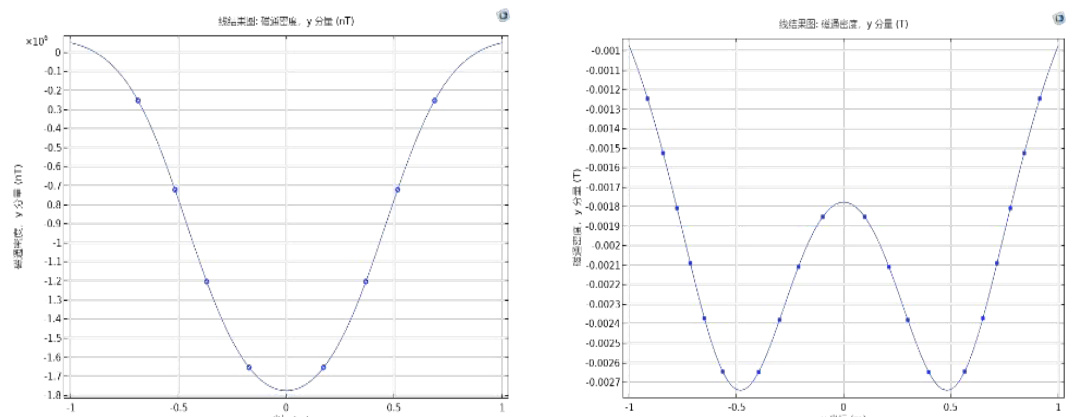
图6(a) 亥姆霍兹线圈磁场随轴向与径向坐标的变化


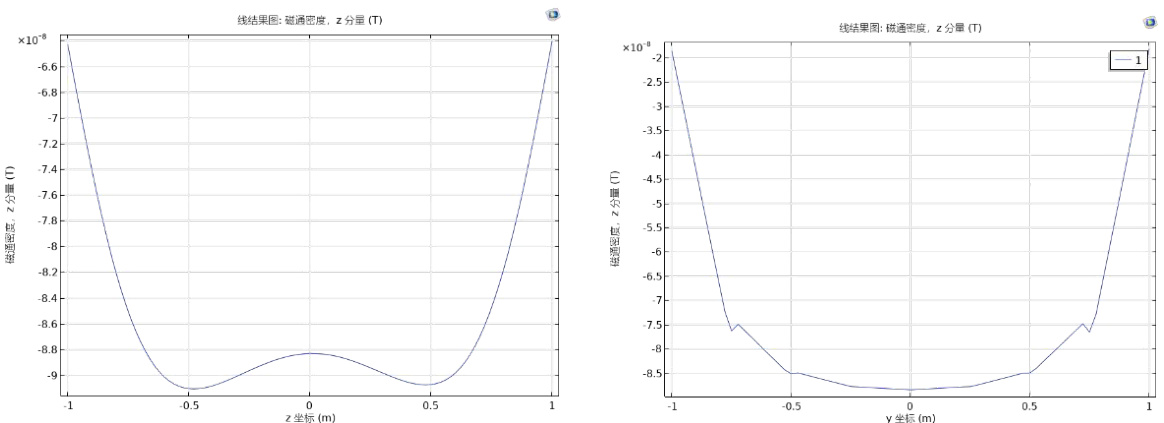
图6(b) 等距球形线圈磁场随轴向与径向坐标的变化


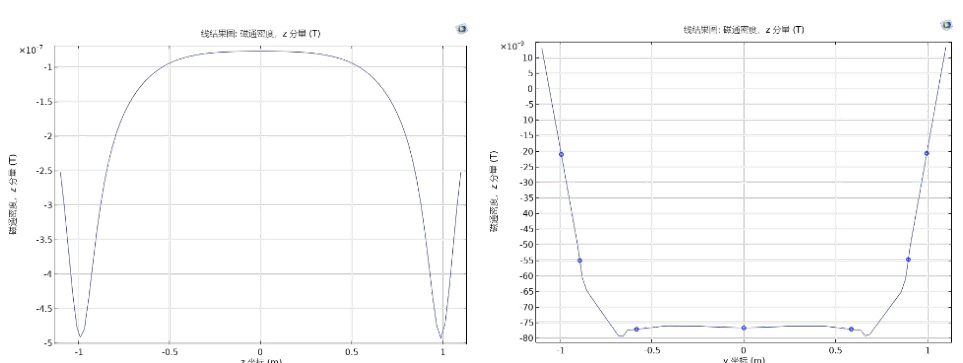
图6(c) 优化球形线圈磁场随轴向与径向坐标的变化

3.2 磁场均匀性分析

利用模型仿真计算三种线圈的 磁场均匀区（即磁场大小相较中心点的变化不超过 的空间），发现优化球形线圈相较于其他二者有更大的径向均匀区，优化作用显著，见表2。

表2 三种线圈的 磁场均匀区

其中，轴向占比指平行于线圈中心轴线方向（即沿 方向）的均匀区占比（见图7），

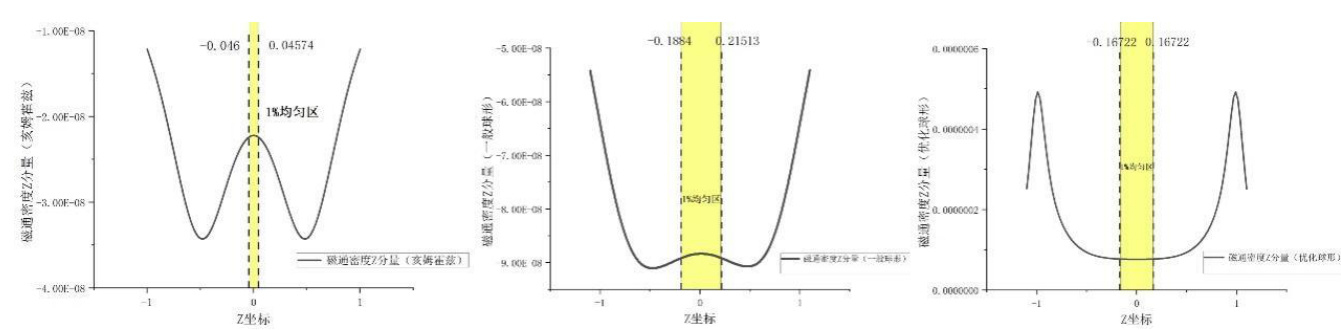
径向占比指垂直于线圈中心轴线方向（即沿r 方向）的均匀区占比（见图8）。

图7 轴向均匀区大小示意图

从左到右依次为（a）亥姆霍兹线圈、（b）等距球形线圈和（c）优化球形线圈。横坐标为线圈轴线上各点的 坐标，纵坐标为磁感应强度 。黄色填充区域即为磁场的轴向 均匀区。


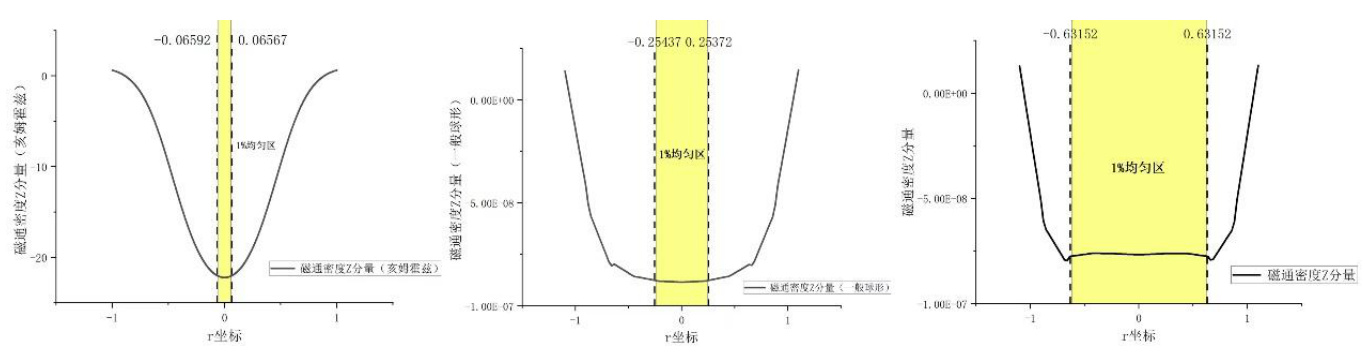
图8 径向均匀区大小示意图

从左到右依次为（a）亥姆霍兹线圈、（b）等距球形线圈和（c）优化球形线圈。横坐标为沿线圈直径方向上各点的 坐标，纵坐标为磁感应强度 。黄色填充区域即为磁场的径向 均匀区。

在同样的条件下，亥姆霍兹线圈在 方向的 均匀区占比为 ，在 方向占比为 等距球形线圈在 方向的 均匀区占比为 ，在 方向占比为 ；优化后的线圈在 方向的 均匀区占比为 ，在 方向占比为 。

结合以上数据，本项目的优化球形线圈对径向均匀区有很大的提升，其相对等距球形线圈的扩大比达到了 $ ，极大地完成了均匀化的任务。

结论

本文提出了一种基于多变量分析和改进PSO 算法的线圈阵列的设计方法，其目的在于产生高度均匀的均匀场。通过多变量的分析以及泰勒展开的方式，得到了含有约束条件的线圈数学模型，并针对数学模型完成了PSO 的改进，得到了线圈参数。与传统方法相比，均匀度有了明显提高，通过对亥姆霍兹线圈与普通球线圈的仿真模拟，发现本设计均匀性分别提升1 至2 倍。基于球形的设计的特性，本设计完全可以拓展至二维乃至三维，进而可以在不同空间条件下提供轴向均匀的磁场，可以满足高精度磁强计的应用要求。

本设计在继承了前人用途的同时，极大地扩展了性能，如果应用于磁导航以及磁标定、磁测量领域，对于精度的提升是前所未有的，并且三维化，小型化的设计令其可以被更广泛应用于其他类型的仪器中，可以助力于其他方面磁场科学的进步。

参考文献

[1]王倩，周晓华，朱强，辛督强．关于产生均匀磁场的亥姆霍兹线圈的研究[J]．大学物 理实验，2022，35（03）
[2]Jian Wang, Shouxian She, Sijiong Zhang. An improved Helmholtz coil and analysis of its magnetic field homogeneity. Rev. Sci. Instrum. 1 May 2002; 73 (5)
[3]张引科，昝会萍．共轴三线圈磁场的均匀性[J]．大学物理，2004，23(6)
[4]黄兆梁．Helmholtz 线圈与共轴三线圈磁场均匀性分析[J]．常州工学院学报，2014， 27(06)
[5]胡朝晖，穆维维，吴文峰，周斌权．产生匀强磁场的圆柱形线圈组设计方法[J]．北京 航空航天大学学报，2018，44(03)
[6]LYU Zhifeng，ZHANG Jinsheng，WANG Shicheng，et al．Optimal design of multi-coil system for generating uniform magnetic field based on intelligent optimization algorithm and finite element method．Journal of Beijing University of Aeronautics and Astronautics，2019， 45(5)
[7] J. E. Everett and J. E. Osemeikhian. Spherical coils for uniform magnetic fields, J. Sci. Instrum., vol. 43, no. 7, pp. 470–474, Jul. 1966
[8] H. Pang et al., Design of Highly Uniform Three Dimensional Spherical Magnetic Field Coils for Atomic Sensors, in IEEE Sensors Journal, vol. 20, no. 19, pp. 11229-11236, 1 Oct.1, 2020